비트(bit)와 바이트(byte)
컴퓨터에서 데이터를 표현하는 단위를 비트와 바이트로 구분할 수 있다.

위 그림은 컴퓨터가 인식하는 데이터를 그림으로 나타낸 것이다.
0과 1을 표현하는 하나의 단위를 1비트라고 표현하고 8개의 비트가 모여서 1바이트가 된다.
1개의 비트로 표현할 수 있는 정보는 0 과 1 2개이므로 1바이트가 표현할 수 있는 정보의 수는 2의 8제곱 즉 256 가지이다.
따라서 1바이트 크기인 char형이 -128~127까지 총 256가지의 숫자가 표현 가능한 것이다.
2진수 정수

정수는 다음과 같은 형태로 표현이 된다.
맨 앞에 있는 수를 '가장 중요한 비트'라는 의미의 MSB (Most Significant Bit) 라 하는데
이 수가 0이면 양수, 1이면 음수를 나타낸다.
따라서 위 그림에서 표현한 수는 41이다.
그런데 -41을 표현하는 방식은 부호만 바꿔서 결정되는 것이 아니다.
예를 들어 '0000 0101'이라는 수와 MSB만 바꾼 '1000 0101'을 컴퓨터가 연산하는 방식으로
각 비트 자리를 모두 더하면 '1000 1010' 이 되고 이는 0 이 아니다.

어떤 수의 부호를 바꾸고 싶으면 0을 만들기 위해 그 수의 모든 비트를 보수를 취한 후 1을 더해주어야 한다.
예를 들어 -41 은 '0010 1001'의 보수인 '1101 0110'에 1을 더한 '1101 0111' 이 된다.
여기서 0010 1001 과 1101 0111의 각 자리 비트를 모두 더하면 '1 0000 0000' 이 되고
제일 앞자리의 1은 1바이트를 초과하므로 버려지게 되어 0 이된다.
따라서 음수를 10진수 정수로 구할 때에는 바로 구할 수 없고 모든 비트를 보수를 취한 후 1을 더해주어서
절댓값(크기)을 구해주어야 한다.
2진수 실수

실수는 2진수로 다음과 같은 형태로 표현이 된다.
2바이트의 실수는 1비트를 부호, 7비트를 지수, 그리고 남은 8비트를 소수점 ( m 값 ) 을 표현하는 데 사용한다.
0.0을 표현하려면 e와 m 값에 0을 대입하여
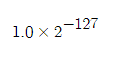
으로 표시하게 되지만 이것은 0과 가까운 값일 뿐 0이 되지 않는다.
이렇게 발생한 소수점의 오차를 부동소수점 오차라고 한다.
실수는 이런 식으로 복잡하게 표현되지만 오히려 오차가 존재하게 된다.
그럼에도 이러한 방식을 사용하는 것은 부동소수점 오차는 매우 작은 값이기 때문에
보통 사용자가 신경 쓸 필요가 없고 더 적은 비트로 더 많은 값을 표현할 수 있기 때문이다.
예를 들어 1비트에 부호, 7비트에 소수점 이상, 나머지 8비트에 소수점 이하를 할당하게 되면
실수는 2바이트로 정수 부분은 -128~127, 소수 부분은 -0.256~0.255 밖에 표현할 수 없을 것이다.
이는 최대 소수점 이하 3자리까지밖에 표현할 수 없으며 그마저도 완벽하지 않다.
비트 연산
비트 연산은 주로 하드웨어 관련 프로그래밍에서 주로 사용되지만 메모리의 효율성을 위해 사용되기도 한다.
비트 연산에 사용되는 비트 연산자의 종류는 다음 표와 같다.
|
연산자
|
연산자의 기능
|
결합 방향
|
|
&
|
비트 단위로 AND 연산을 시행
|
→
|
|
|
|
비트 단위로 OR 연산을 시행
|
→
|
|
^
|
비트 단위로 XOR 연산을 시행
|
→
|
|
~
|
피연산자의 모든 비트를 반전시킴
|
←
|
|
<<
|
피연산자의 비트 열을 왼쪽으로 이동
|
→
|
|
>>
|
피연산자의 비트 열을 오른쪽으로 이동
|
→
|
1) & 연산자 ( 둘 다 1이어야 1을 반환 )
0 & 0 // 0을 반환
0 & 1 // 0을 반환
1 & 1 // 1을 반환
2) | 연산자 ( 하나라도 1 이면 1을 반환 )
0 | 0 // 0을 반환
0 | 1 // 1을 반환
1 | 1 // 1을 반환
3) ^ 연산자 ( 값이 서로 다를 때 True를 반환 )
0 | 0 // 0을 반환
0 | 1 // 1을 반환 ( True )
1 | 1 // 0을 반환
4) << 연산자
num1 << a // num1의 비트를 a 칸씩 왼쪽으로 이동
num1 >> a // num1의 비트를 a 칸씩 오른쪽으로 이동
*비트의 이동으로 인해서 생기는 빈칸에는 0으로 채워지고
이동으로 인해 밀려나는 데이터는 그냥 버려진다.
다음 연산자들의 작동 방식의 예시를 코드로 작성해보겠다.
#include <stdio.h>
int main ()
{
int num1 = 15; // 00000000 00000000 00000000 00001111 = 15
int num2 = 20; // 00000000 00000000 00000000 00010100 = 20
int res1 = num1 & num2; // 00000000 00000000 00000000 00000100 = 4
int res2 = num1 | num2; // 00000000 00000000 00000000 00011111 = 31
int res3 = num1 ^ num2; // 00000000 00000000 00000000 00011011 = 27
int res4 = ~num1; // 11111111 11111111 11111111 11110000 = -36
int res5 = num2 >> 4; // 00000000 00000000 00000000 00000001 = 1
int res6 = num2 << num1; // 0000000 00001010 00000000 00000000 = 655368
printf("%d %d %d %d %d %d", res1, res2, res3 ,res4, res5, res6);
return 0;
}
<< 연산자 혹은 >> 연산자를 사용하였을 때 MSB의 숫자가 1에서 0으로 바뀌게 되면
부호를 유지하기 위해 1을 채우는 경우도 있고 부호에 상관없이 0을 채우는 경우도 있다.
이 경우는 CPU와 컴파일러에 따라 다르다.
이를 확인하는 코드를 작성해보겠다.
#include <stdio.h>
int main ()
{
int test = -16; // 11111111 11111111 11111111 11110000
int res = 0;
res = test >> 2; /* 예상 결과 값
00111111 11111111 11111111 11111100 ( 0이 채워짐 ) = 1073741820
11111111 11111111 11111111 11111100 ( 1이 채워짐 ) = -4 */
printf("%d", res);
return 0;
}
'C언어 > C언어 문법' 카테고리의 다른 글
| [C언어] 형변환 (Type Casting) (0) | 2024.02.07 |
|---|---|
| [C언어] 연산자 (산술, 대입, 관계, 논리, 복합대입, 증강 연산자) (0) | 2024.01.26 |
| [C언어] sizeof 함수 (0) | 2024.01.23 |
| [C언어] 필드 폭 지정 (0) | 2024.01.23 |
| [C언어] 이스케이프 시퀀스 (Escape Sequence) (0) | 2024.01.23 |


